Cara Mencari Keliling Lingkaran Jika Diketahui Luas

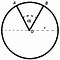
Unsur-Unsur Lingkaran

Dirangkum dari “Buku Pintar Bimbel SMP Kelas 7, 8, 9” oleh Budi Lintang S.Pd.I, berikut unsur-unsur lingkaran.

Gambar lingkaran (Katadata)

Titik pusat lingkaran adalah titik yang terletak di tengah-tengah lingkaran. Pada gambar datas, titik O adalah titik pusat lingkaran.

Jari-jari lingkaran adalah garis dari titik pusat lingkaran ke lengkungan lingkaran. Pada gambar, jari-jari lingkaran ditunjukkan oleh garis OA, OB, dan OC.

Diameter adalah garis lurus yang menghubungkan dua titik pada lengkungan lingkaran dan melalui titik pusat. Garis AB pada lingkaran O merupakan diameter lingkaran tersebut. Perhatikan bahwa BC =BO + OC. Dengan demikian, nilai diameter merupakan dua kali nilai jari-jari, maka d = 2r.

Dalam lingkaran, busur adalah garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titik sebarang di lengkungan tersebut. Dalam gambar, garis lengkung AC, CB, dan AB adalah busur lingkaran.

Tali busur lingkaran adalah garis lurus dalam lingkaran yang menghubungkan dua titik pada lengkungan lingkaran. Berbeda dengan diameter, tali busur tidak melalui titik pusat lingkaran O. Tali busur lingkaran tersebut ditunjukkan oleh garis lurus AC yang tidak melalui titik pusat pada gambar tersebut.

Tembereng adalah luas daerah dalam lingkaran yang dibatasi oleh busur dan tali busur. Daerah yang dibatasi oleh busur AC dan tali busur AC adalah tembereng.

Juring lingkaran adalah luas daerah dalam lingkaran yang dibatasi oleh dua buah jari-jari lingkaran dan sebuah busur yang diapit oleh kedua jari-jari lingkaran. Pada gambar, juring lingkaran ditunjukkan oleh daerah yang diarsir dan dibatasi oleh jari-jari OA dan OB serta busur AB, dinamakan juring BOA.

Apotema merupakan garis yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran tersebut. Garis yang dibentuk bersifat tegak lurus dengan tali busur.

Rumus keliling lingkaran

Guna menghitung keseluruhan panjang sisi dari lingkaran, kamu perlu menghitung menggunakan rumus keliling lingkaran. Untuk cara menghitung keliling lingkaran, bisa menggunakan jari-jari atau ukuran diameter yang biasanya telah disebutkan di soal.

Adapun rumus keliling lingkaran adalah

K Lingkaran = π x d (jika yang diketahui adalah diameter) atau

K Lingkaran = π x 2r (apabila yang disebutkan dalam soal adalah jari-jari)

π phi = bisa 3,14 atau 22/7

r = jari-jari lingkaran

d = diameter lingkaran

Karena π ada dua opsi yang bisa dipilih, maka sesuaikan dengan panjang jari-jari atau diameternya, ya. Apabila salah satunya merupakan kelipatan tujuh (7, 14, 21, dan seterusnya), maka gunakan 22/7. Namun, apabila bukan kelipatan tujuh, akan lebih mudah jika pakai 3,14.

Baca Juga: Aturan Sinus dan Cosinus dalam Trigonometri Matematika

Konsep Jari-Jari dan Diameter Lingkaran

Jari-jari dan diameter rupanya masih sering bikin sebagian oleng. Alias, nggak teliti saat mengerjakan soal. Akibatnya, banyak juga yang tertukar antara rumus jari-jari dan rumus diameter.

Padahal, keduanya sangat berbeda, lho, Skollamate. Memang sama-sama unsur lingkaran yang nggak jauh dari titik pusat, tapi jari-jari dan diameter memiliki definisi yang berbeda, yakni:

Nah, sudah lebih tercerahkan tentang perbedaan jari-jari dan diameter? Kalau belum, simak contoh soalnya berikut ini, deh.

Diketahui panjang diameter sebuah lingkaran adalah 20 cm, berapa jari-jarinya?

Jari-jari dari sebuah sebuah lingkaran dengan panjang diameter 20 cm adalah 10 cm.

Nah, itu dia contoh soal untuk mencari jari-jari jika yang diketahui adalah ukuran diameternya. Sekarang, coba kita balik dengan contoh berikut.

Diketahui panjang jari-jari sebuah lingkaran adalah 16 cm, berapa diameternya?

Diameter dari sebuah sebuah lingkaran dengan panjang jari-jari 16 cm adalah 32 cm.

Apakah sudah cukup jelas? So pasti sudah terasa menyenangkannya sampai sini, ya? Tapi, nggak cukup sampai di pembahasan jari-jari dan diameter. Ada yang makin menantang dan seru terkait rumus lingkaran lainnya, yaitu cara mencari tahu rumus keliling lingkaran dan luas lingkaran.

Rumus Keliling Lingkaran

Sebuah lingkaran membentuk garis lengkung dengan panjang tertentu yang disebut keliling.

Rumus keliling lingkaran adalah K = 2 x π x r atau K = π x d

K: Keliling lingkaran

r: Jari-jari lingkaran

Adapun rumus Keliling ¾ Lingkaran adalah K = r + r + busur 3/4 lingkaran atau K = 2r + (¾ x π x d)

Sebuah lingkaran mempunyai diameter 28 cm maka keliling lingkaran tersebut adalah…

Maka, hasil keliling lingkaran adalah 88 cm².

Sebuah lingkaran memiliki jari-jari 20 cm, berapa keliling lingkaran tersebut?

Rumus Luas Seperempat Lingkaran

Rumus luas seperempat lingkaran adalah L = ¼ × luas lingkaran atau ¼ × π × r × r.

Jika garis tengah sebuah lingkaran 16 m, maka luas seperempat lingkarannya adalah…

Diketahui garis tengah atau diameter sepanjang 16 m, maka jari-jarinya adalah 8 m.

Luas ¼ lingkaran = ¼ × π × r × r = ¼ × 3,14 × 8 × 8 = 50,24 m2.

Maka, luas seperempat lingkaran tersebut adalah 50,24 m2.

Contoh soal keliling lingkaran dengan diameter

Danial sedang berenang di kolam berbentuk lingkaran. Sebelum mengitarinya, ia terlebih dahulu ingin mengetahui keliling lingkaran. Apabila diketahui diameternya sepanjang 20 meter, maka berapa kelilingnya?

Yang diketahui dari soal adalah diameter. Maka, menggunakan rumus Keliling Lingkaran = π x d. Kedua, karena panjang diameter bukanlah kelipatan tujuh, maka phi yang digunakan adalah 3,14. Adapun tahapan menghitungnya yakni:

Nah, panjang keliling kolam yang hendak diputari Danial adalah 62,8 meter.

Skollamate, ketika pertama kali mendengar lingkaran, apa yang ada di pikiranmu? Hmm… Ban sepeda, kancing, jam dinding, atau pizza? Betul! Pasti kamu bisa menyebutkan banyak benda berbentuk lingkaran.

Tahukah kamu kalau benda yang kamu sebutkan tadi adalah gerbang dari sebuah konsep ilmu Matematika?

Ya! Tanpa kamu sadari, dulu kamu mengenal lingkaran hanya sebagai jenis “bentuk”. Tapi sekarang, kamu akan mengenal lingkaran lebih jauh lagi sebagai salah satu dari konsep Matematika, yaitu “bangun datar”. Menarik, kan?

Nggak sebatas bentuknya melingkar, kamu akan lebih tau serba-serbi tentang lingkaran. Kamu juga bakal ketemu rumus lingkaran yang nggak cuma ada satu. Penasaran mau pelajarin lebih lanjut? Yuk, baca di artikel ini!

Sifat-Sifat Lingkaran

Dirangkum dari Buku Ajar Geometri Dan Pengukuran Berbasis Pendekatan Saintifik, sifat-sifat lingkaran adalah:

Demikian pembahasan tentang rumus luas lingkaran, cara menghitung, dan contoh soal.

Apa, sih, lingkaran? Iya, yang bulat itu. Dilansir e-Gmat, lingkaran adalah bangun geometris yang terbentuk dari kumpulan titik pada jarak tetap. Lingkaran termasuk dalam bangun datar yang unik, sebab hanya punya satu lengkung dan gak ada titik sudut, layaknya bentuk lain.

Saat mempelajari bentuk geometri ini, kamu akan bertemu dengan rumus keliling lingkaran hingga luas bangun datar. Sebelumnya, akan lebih mudah kalau kamu memahami istilah-istilah yang menyusun bangun lingkaran nantinya dari cara menghitung keliling lingkaran hinga contoh soal keliling lingkaran akan dibahas dibawah ini. Apa saja?

Lingkaran adalah bangun datar yang tersusun dari titik-titik yang berjarak sama dari satu titik pusat. Jarak umum dari pusat lingkaran ke titik-titiknya disebut jari- jari. Jadi, secara keseluruhan, susunan lingkaran bergantung pada pusatnya (O) dan jari-jarinya (R).

Kalau mengamati sekitar, ada banyak benda yang berbentuk lingkaran. Yup, ada jam dinding, piring, alas gelas, hula hoop, dan masih banyak lainnya. Semuanya memiliki bentuk yang sama dan gak punya titik sudut.

Nah, ternyata, lingkaran gak sesederhana garis panjang yang melingkar, lho. Ada banyak istilah dalam bangun dua dimensi ini yang perlu kamu ketahui sebelum menghitung kelilingnya.

Agar lebih mudah memahaminya, kamu bisa melihat gambar di atas, ya.

Rumus Luas Setengah Lingkaran

Adapun rumus luas setengah lingkaran adalah (π x r x r)/2.

Sebuah lingkaran memiliki jari-jari 10 cm, maka luas setengah lingkaran adalah…

Rumus setengah lingkaran adalah (π x r x r)/2.

Maka L = (3,14 x 10 x 10)/2 = 157 cm2.

Jadi, luas setengah lingkaran tersebut adalah 157 cm2.

Sudut Pusat dan Keliling Lingkaran

Sudut pusat adalah sudut yang dibentuk oleh dua buah jari-jari lingkaran. Ukuran sudut pusat sama dengan dua kali sudut keliling. Sedangkan sudut keliling adalah sudut yang terbentuk dari dua buah tali busur yang berpotongan pada keliling sebuah lingkaran.

Sudut keliling lingkaran dibedakan menjadi: